1. Two Sum

Array

Hash Table

Description

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example

Input : nums = [2,7,11,15], target = 9

Output : [0,1]

Explanation :

Because nums[0] + nums[1] == 9, we return [0, 1].

Intuition

In this question we find out two different indices it's value sum is given target value
nums[i] + nums[j] = target here i != j

Approaches

Brute Force

One brute force approach is to consider every pair of elements and check if their sum equals the target.
We need to find out two different indices that sum is target value so we take one by one ith indices and one by one jth indices and check it's sum is equal to target value.
We take two for loops one is for traveling i indices and second one is traveling j indices.

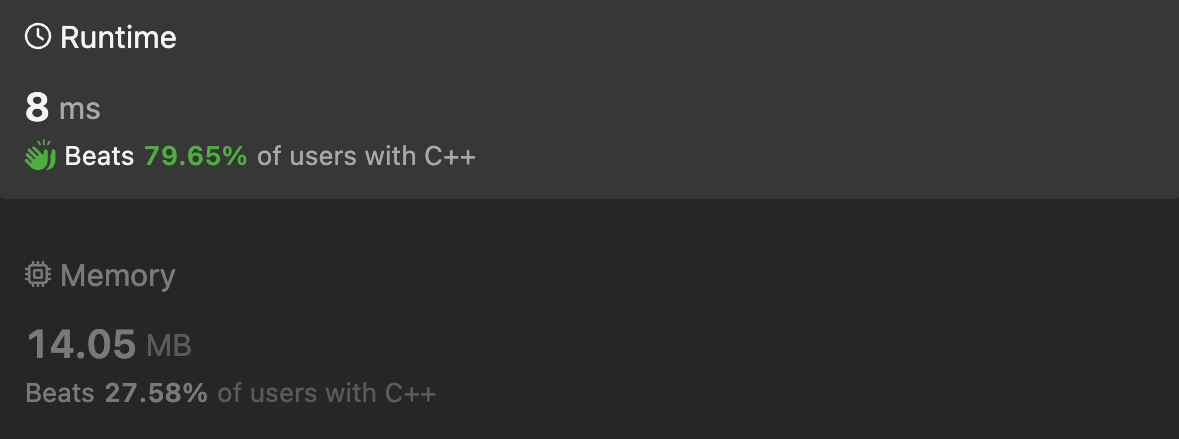
Time Complexity

O(N * N) where 'N' is nums length

Space Complexity

O(1)

Code

two-sum.cpp

class Solution {
public:
  vector<int> twoSum(vector<int>& nums, int target) {
    int n = nums.size();
    for (int i = 0; i < n; i++) {
      for (int j = i + 1; j < n; j++) {
        if (nums[i] + nums[j] == target)
          return {i, j};
      }
    }
    return {}; // solution not found
  }
};

Analysis

Using Hash Table

We have this equation nums[i] + nums[j] = target
nums[j] = target - nums[i]
In one pass we have target and nums[i] so using above formula and hash table we find nums[j].
Each iterator we store index value and index at hash table table[nums[i]] = i
At each index we check table[target - nums[i]] is present if present then we return {i, table[target - nums[i]]}

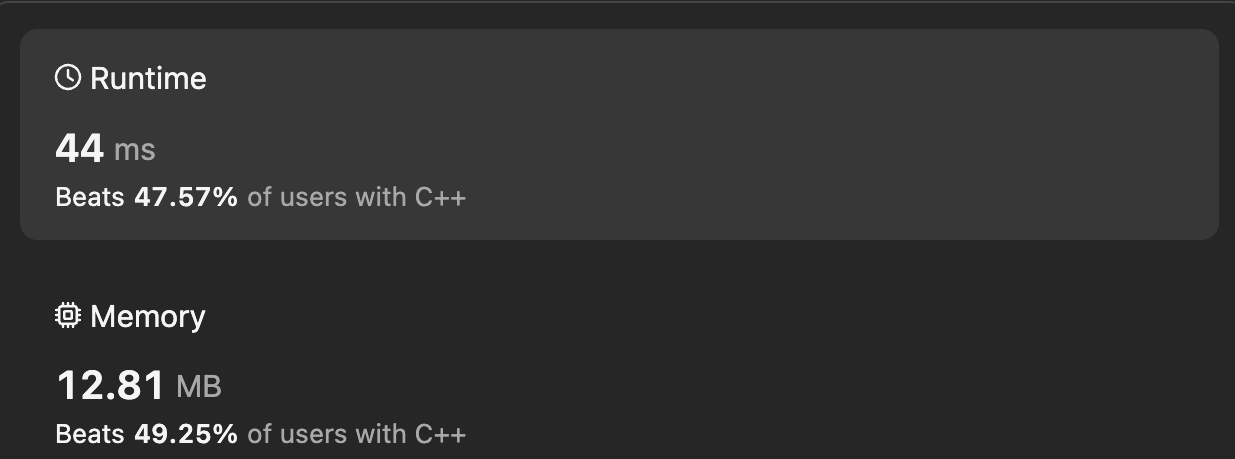
Time Complexity

O(N) where 'N' is nums length

Space Complexity

O(N)

Code

two-sum.cpp

class Solution {
public:
  vector<int> twoSum(vector<int>& nums, int target) {
    int n = nums.size();
    unordered_map<int, int> table;
 
    for (int i = 0; i < n; i++) {
      if(table.find(target - nums[i]) != table.end())
        return {i, table[target - nums[i]]};
      table[nums[i]] = i;
    }
 
    return {}; // solution not found
  }
};

Analysis