LC Solutions

621. Task Scheduler

Array
Hash Table
Sorting
Counting

Description

You are given an array of CPU tasks, each represented by letters A to Z, and a cooling time, n. Each cycle or interval allows the completion of one task. Tasks can be completed in any order, but there's a constraint: identical tasks must be separated by at least n intervals due to cooling time.

Return the minimum number of intervals required to complete all tasks.

Example

Input

tasks = ['A', 'A', 'A', 'B', 'B', 'B', 'C', 'C', 'C', 'D', 'D', 'E'], n = 2

Output 12
Explanation

    A possible sequence is: A -> B -> C -> A -> B -> C -> D -> A -> B -> D -> C -> A

Intuition

  • We need to do task every interval at max 1 and similar task will do after n interval.
  • So we need to organize our task and do n interval n different tasks.

Approaches

Brute Force

  • We do first most freq tasks so we optimise our answer.

  • Organise task as most freq at first

    621-1

  • Then do n + 1 tasks because next task will do any taking ideal time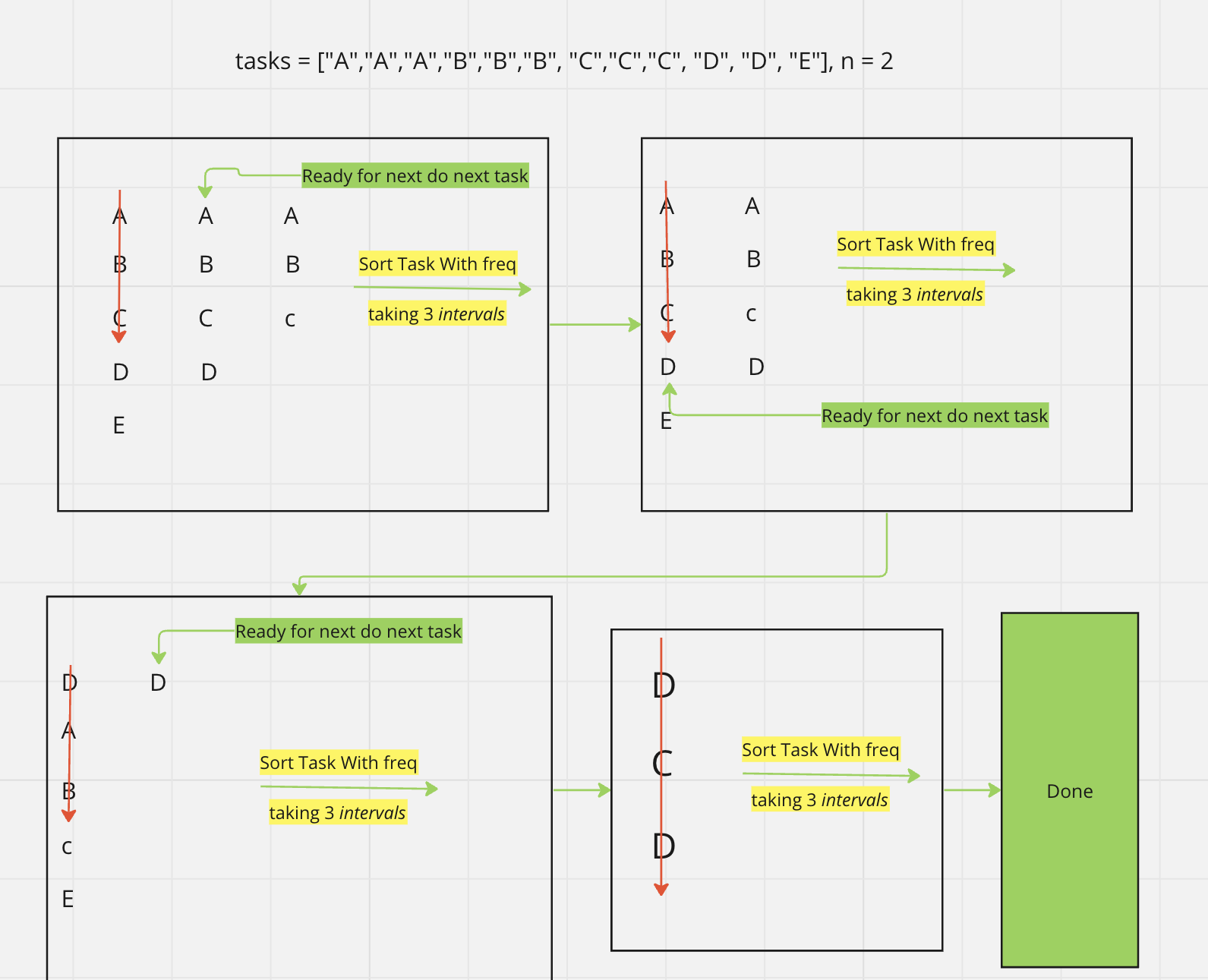

    621-2

Time Complexity

  • O(N * 26 * log(26)) where 'N' is points length

Space Complexity

  • O(1)

Code

cpp
class Solution {
public:
  int leastInterval(vector<char>& tasks, int n) {
      vector<int> f(26);
      for(auto &t : tasks) f[t - 'A']++;
 
      int ans = 0, ttl_tasks = tasks.size();
 
      while(ttl_tasks > 0) {
        sort(f.rbegin(), f.rend());
        int cnt_tasks = 0;
        for(int i = 0; i < 26 && cnt_tasks <= n; i++) {
          if(f[i]) {
              f[i]--;
              ttl_tasks--;
              cnt_tasks++;
          }
        }
        ans += cnt_tasks;
        if(ttl_tasks > 0) ans += n + 1 - cnt_tasks;
      }
      return ans;
  }
};

Analysis

aalysis

Using Math

Code

class Solution {
public:
  int leastInterval(vector<char>& tasks, int n) {
    vector<int> mp(26);
    int count = 0;
    for(auto &t : tasks)
        count = max(count, ++mp[t - 'A']);
 
    int ans = (count - 1) * (n + 1);
    for(auto &cnt : mp)
        if(cnt == count) ans++;
 
    return max((int)tasks.size(), ans);
  }
}

Happy Coding 😀